Here, in no particular order, are the most common airblast-related questions:
- What nozzles should I use?
- How do I adjust my air settings?
- How much volume should I use?
- How fast should I drive?
The first three questions have long answers that are covered throughout the website and in Airblast101. Travel speed, however, is easy: Drive slow enough to allow the spray-laden air to reach and displace the air in the target canopy, but fast enough to get the job done in a timely manner.
In a 2010 survey of airblast sprayer operators in Ontario, the average ground speed was about 5 km/h (~3.1 mph). Responses spanned from 3 km/h to 7.5 km/h.
So why doesn’t the article end here?
Because operators must know their average travel speed to calculate how much spray mix and time is required to finish the job. Notice that it’s an average – not a constant. Speed changes on hills, when ground conditions change, as the sprayer gets lighter, and when the operator responds to weather or canopy size.
You may be tempted to consult the tractor speedometer, but it can be fooled by changes in wheel size, tire wear or slippage. If you rely on a rate controller, know that monitoring wheel rotations is less accurate than employing RTK satellite navigation for similar reasons.
My preference is to fill the sprayer 1/2 full of water, download any free speedometer app for your smartphone, and then drive your operation with the fan on and the spray off. Consult the phone for your average speed for each pass. Take a screen shot and email it to yourself as a time-stamped component of your spray records.

Those that prefer a manual method can follow the classic protocol for determining average travel speed.
- Go to a row that is representative of the terrain in your planting. Measure out a distance of 50m or 150ft depending whether you prefer metric or US Imperial units and mark the start and finish positions with wire marker flags.
- Fill the sprayer tank half full of water.
- Select the gear and engine speed in which you intend to spray. If using a pull-behind sprayer, ensure the PTO is running or you could introduce errors.
- Bring the sprayer up to speed for a running start and begin timing as the front wheel passes the first flag. This is far easier when there are two people.
- Stop the timer as the front wheel passes the second flag.
- Stay out of any ruts and run the course two more times.
- Determine the average drive time for the three runs (i.e. the sum of all three times in seconds divided by three).
- Finally, Calculate travel speed using one of the following formulae, again depending on preferred units:
Ground Speed (km/h) = Average drive time for 50m (s) ÷ 13.9 (a constant)
Ground Speed (mph) = Average drive time for 150ft (s) ÷ 220 (a constant)
How fast is too fast?
If you’re an airblast operator, you’re pressed for time. Common practice is to drive faster to complete the job more quickly. But, that can compromise coverage and increase drift; It takes time for spray-laden air to reach and then displace the air in the target canopy.
We ran an orchard demo to explore the effects of travel speed on coverage. We placed a regularly-spaced series of water sensitive papers across the width of a large and a small apple canopy. Then, we used a 3-point hitch sprayer to apply 500 L/ha (adjusted for travel speed) at 2.5 km/h and 5.5 km/h.
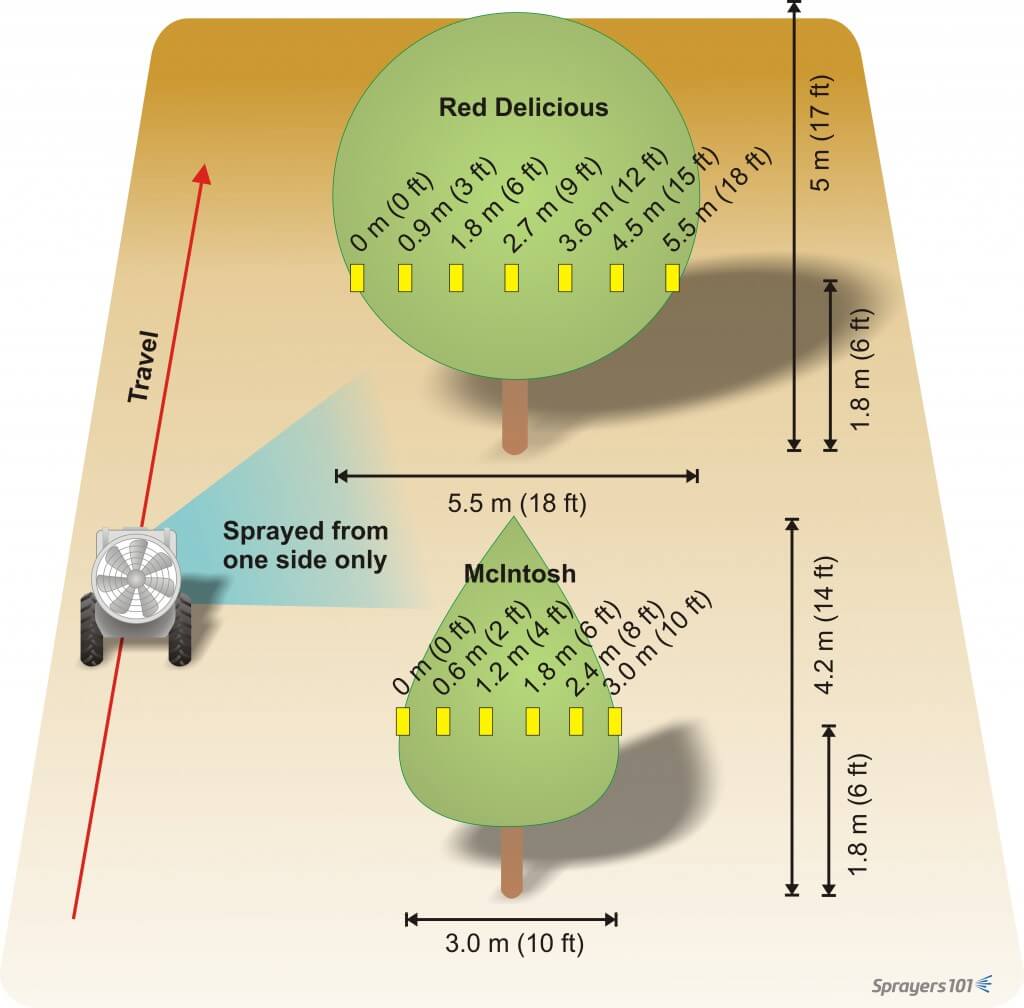
We collected the papers and used a digital scanner to determine the percent coverage and the droplet density (i.e. droplet count per square centimeter). We graphed the results and, to no great surprise, found that the slower travel speed resulted in higher droplet densities further into the canopies.
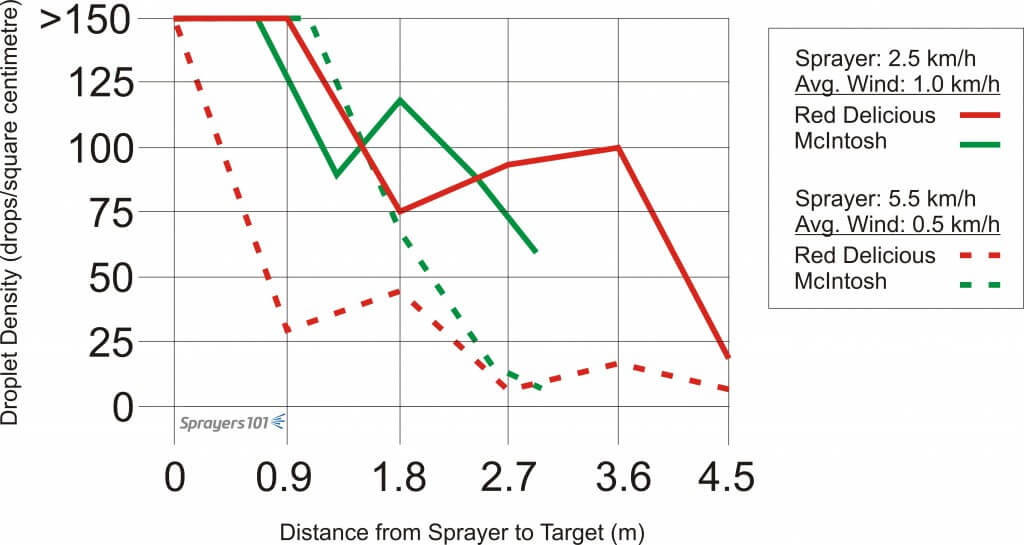
This relationship between travel speed and coverage is fairly consistent. We promote the ribbon test to indicate if you’re accomplishing your goal. The ribbon test will indicate if your speed is appropriate for the circumstances. If the ribbons flutters as you drive by, great! If the canopy is open, the weather is good and the ribbons don’t move no matter how slow you drive, you’ll have to change your air settings
